程序员的算法课（17）-常用的图算法：深度优先（DFS）-程序员秋天

一、深度优先搜索介绍

图的深度优先搜索(Depth First Search)，和树的先序遍历比较类似。

它的思想：假设初始状态是图中所有顶点均未被访问，则从某个顶点v出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和v有路径相通的顶点都被访问到。若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

显然，深度优先搜索是一个递归的过程。

二、深度优先搜索图解

1 无向图的深度优先搜索

下面以"无向图"为例，来对深度优先搜索进行演示。

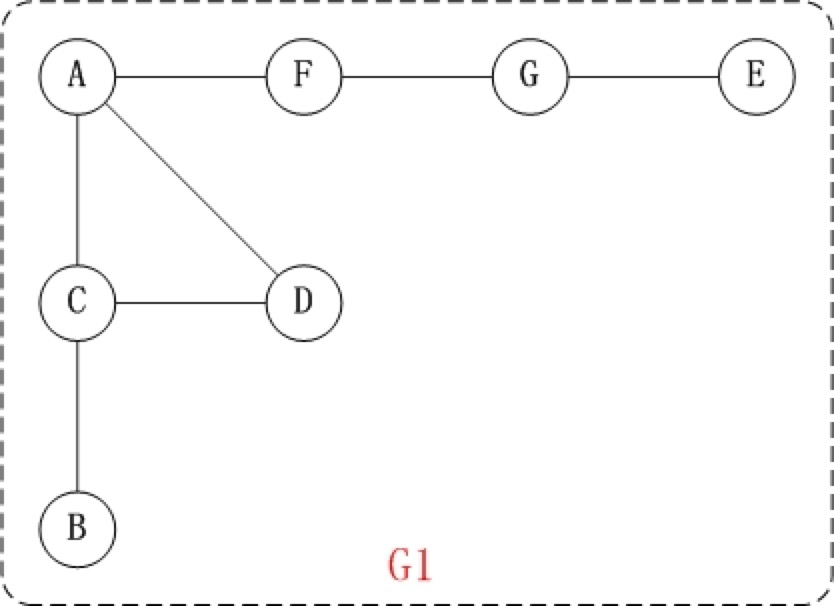
对上面的图G1进行深度优先遍历，从顶点A开始。

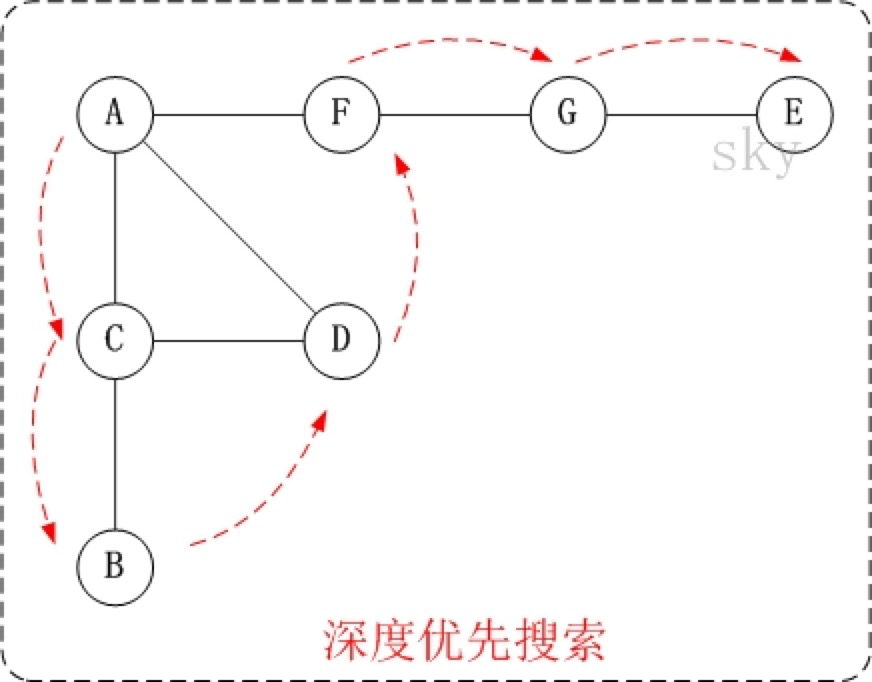
1、 第1步：访问A；
2、 第2步：访问(A的邻接点)C在第1步访问A之后，接下来应该访问的是A的邻接点，即"C,D,F"中的一个但在本文的实现中，顶点ABCDEFG是按照顺序存储，C在"D和F"的前面，因此，先访问C；
3、 第3步：访问(C的邻接点)B在第2步访问C之后，接下来应该访问C的邻接点，即"B和D"中一个(A已经被访问过，就不算在内)而由于B在D之前，先访问B；
4、 第4步：访问(C的邻接点)D在第3步访问了C的邻接点B之后，B没有未被访问的邻接点；因此，返回到访问C的另一个邻接点D；
5、 第5步：访问(A的邻接点)F前面已经访问了A，并且访问完了"A的邻接点B的所有邻接点(包括递归的邻接点在内)"；因此，此时返回到访问A的另一个邻接点F；
6、 第6步：访问(F的邻接点)G；
7、 第7步：访问(G的邻接点)E；

因此访问顺序是：A -> C -> B -> D -> F -> G -> E

2.有向图的深度优先搜索

下面以"有向图"为例，来对深度优先搜索进行演示。

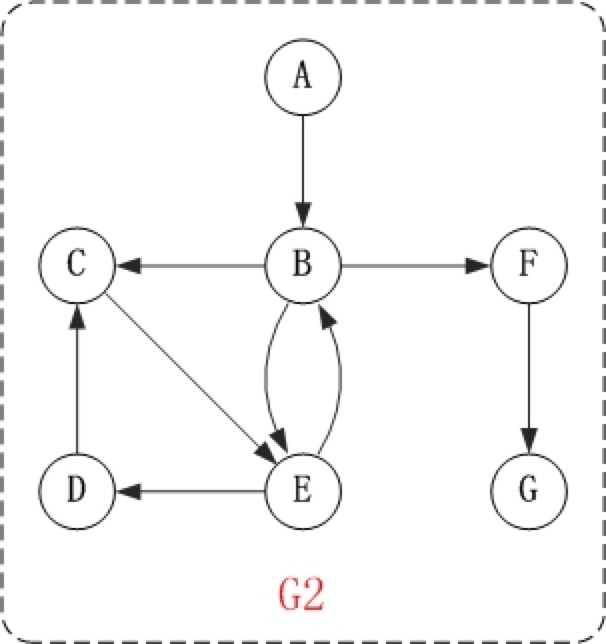
对上面的图G2进行深度优先遍历，从顶点A开始。

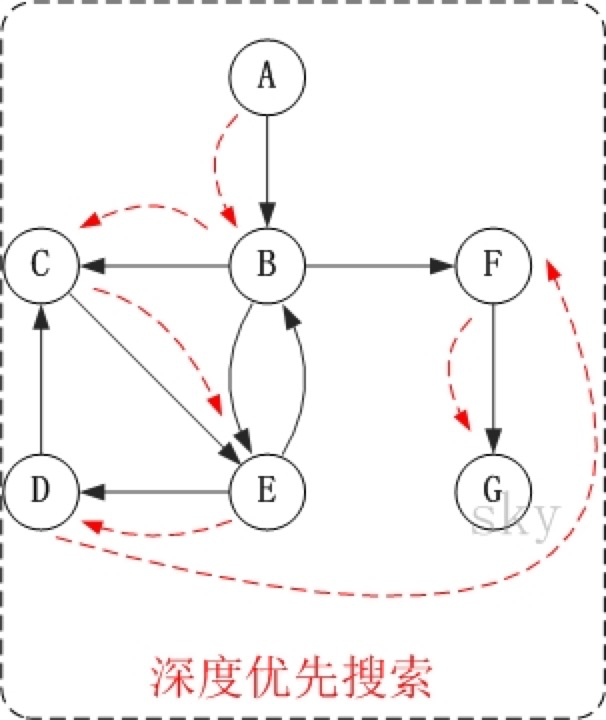
1、 第1步：访问A；
2、 第2步：访问B在访问了A之后，接下来应该访问的是A的出边的另一个顶点，即顶点B；
3、 第3步：访问C在访问了B之后，接下来应该访问的是B的出边的另一个顶点，即顶点C,E,F在本文实现的图中，顶点ABCDEFG按照顺序存储，因此先访问C；
4、 第4步：访问E接下来访问C的出边的另一个顶点，即顶点E；
5、 第5步：访问D接下来访问E的出边的另一个顶点，即顶点B,D顶点B已经被访问过，因此访问顶点D；
6、 第6步：访问F接下应该回溯"访问A的出边的另一个顶点F"；
7、 第7步：访问G；

因此访问顺序是：A -> B -> C -> E -> D -> F -> G

三、代码实现

private boolean[] isVisited = new boolean[vertextSize];

/**
 * 获取指定顶点的第一个邻接点
 * 
 * @param index
 *          指定邻接点
 * @return
 */
private int getFirstNeighbor(int index) {
    for (int i = 0; i < vertexSize; i++) {
        if (matrix[index][i] < MAX_WEIGHT && matrix[index][i] > 0) {
            return i;
        }
    }
    return -1;
}

/**
 * 获取指定顶点的下一个邻接点
 * 
 * @param v
 *          指定的顶点
 * @param index
 *          从哪个邻接点开始
 * @return
 */
private int getNextNeighbor(int v, int index) {
    for (int i = index+1; i < vertexSize; i++) {
        if (matrix[v][i] < MAX_WEIGHT && matrix[v][i] > 0) {
            return i;
        }
    }
    return -1;
}

/**
 * 图的深度优先遍历算法
 */
private void depthFirstSearch(int i) {
    isVisited[i] = true;
    int w = getFirstNeighbor(i);
    while (w != -1) {
        if (!isVisited[w]) {
            // 需要遍历该顶点
            System.out.println("访问到了：" + w + "顶点");
            depthFirstSearch(w); // 进行深度遍历
        }
        w = getNextNeighbor(i, w); // 第一个相对于w的邻接点
    }
}

传0进去，表示v0。
设置v0已访问过，获取v0的第一个邻接点。w != -1说明有这个邻接点，然后对这个临界点进行判断。
已访问，那就找下一个临界点
未访问，进行访问，然后对该邻接点进行深度优先遍历。

四、总结

遍历规则：不断的沿着顶点的深度方向遍历。顶点的深度方向是指它的邻接点方向。
它从图中某个顶点v出发，访问此顶点，然后从顶点的未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到。
简单说，就是顶点将第一个邻接点当作左孩子，其它邻接点都当做右孩子。最后排成一棵树。
深度优先遍历是指先遍历到最深层次，然后再探索邻接点，接着又遍历最深层次。二叉树的先序遍历就是一种深度优先遍历。

我的微信公众号：架构真经（id：gentoo666），分享Java干货，高并发编程，热门技术教程，微服务及分布式技术，架构设计，区块链技术，人工智能，大数据，Java面试题，以及前沿热门资讯等。每日更新哦！

参考资料：

1、 https://blog.csdn.net/Strive_Y/article/details/81810012；
2、 https://www.jianshu.com/p/23b55db1adc0；