程序员的算法课（3）-递归（recursion）算法-程序员秋天

一、什么是递归

递归是一种数学上分而自治的思想。

1、递归将大型复杂问题转化为与原问题相同但规模较小；
2、的问题进行处理；
3、递归需要有边界条件，当边界条件不满足时，递归继续进行；当边界条件满足时，递归停止；

【百度百科】程序调用自身的编程技巧称为递归（ recursion）。递归做为一种算法在程序设计语言中广泛应用。一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。

二、递归的数学表示

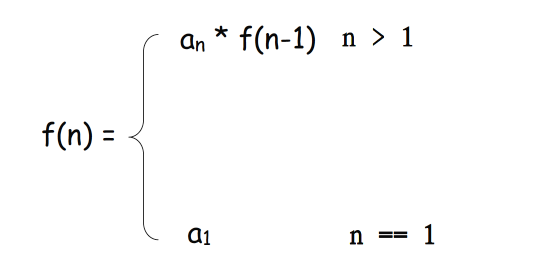
三、一些数学问题的递归解法

1.斐波那契数列

经典数学问题之一；斐波那契数列，又称黄金分割数列，指的是这样一个数列： 1、1、2、3、5、8、13、21、……

这个数列的规律，就是前两项的和是第三项的值，

public class Solution {
    public int Fibonacci(int n) {
        if(n == 0)
            return 0;
        if(n == 1)
            return 1;
        return Fibonacci(n-2) + Fibonacci(n-1);
    }
}

当n比较大时，可以明显感觉算法运行速度比较慢，这是由于上述返回代码中使用了两层递归，使用递归的思想是好的，但是这里我们可以用迭代明显改善算法运行效率，用空间换时间。

public class Solution {
    public int Fibonacci(int n) {
        if(n < 2)
            return n;
        int f = 0, g = 1;
        int result = 0;
        for(int i = 1; i < n; i++){
            result = f + g;
            f = g;
            g = result;
        }
        return result;
    }
}

2.汉诺塔

汉诺塔是一个发源于印度的益智游戏，也叫河内塔。相传它源于印度神话中的大梵天创造的三个金刚柱，一根柱子上叠着上下从小到大64个黄金圆盘。大梵天命令婆罗门将这些圆盘按从小到大的顺序移动到另一根柱子上，其中大圆盘不能放在小圆盘上面。当这64个圆盘移动完的时候，世界就将毁灭。

public class Hanoilmpl {

    public void hanoi(int n, char A, char B, char C) {
        if (n == 1) {
            move(A, C);
        } else {
            hanoi(n - 1, A, C, B);//步骤1 按ACB数序执行N-1的汉诺塔移动
            move(A, C);             //步骤2   执行最大盘子移动
            hanoi(n - 1, B, A, C);//步骤3 按BAC数序执行N-1的汉诺塔移动
        }
    }

    private void move(char A, char C) {//执行最大盘子的从A-C的移动
        System.out.println("move:" + A + "--->" + C);
    }

    public static void main(String[] args) {
        Hanoilmpl hanoi = new Hanoilmpl();
        System.out.println("移动汉诺塔的步骤：");
        hanoi.hanoi(3, 'a', 'b', 'c');
    }
}

3.八皇后问题

八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。

在一个8°¡8国际象棋盘上，有8个皇后，每个皇后占一格；要求皇后间不会出现相互“攻击”的现象，即不能有两个皇后处在同一行、同一列或同一对角线上。

算法思路

初始化：i = 1

初始化：j = 1

从第i行开始，恢复j的当前值，判断第j个位置

a. 位置j可放入皇后：标记位置(i, j)， i++，转步骤2

b. 位置j不可放入皇后：j++, 转步骤a

c. 当j>8时，i--，转步骤3

4.结束：第8行有位置可放入皇后

注意事项：当使用递归的时候，我们需要在执行后将map[row][i] 重新设置为0 ，保证下一次排列的时候棋盘是空的

/**
 * 递归算法之八皇后问题
 *
 * @author Administrator
 */
public class Bahuanghou {
    //定义一个8*8的矩阵
    public static int[][] map = new int[8][8];
    public static int count = 1;

    /**
     * 显示棋盘方法
     */
    public static void show() {
        System.out.println("第" + count + "中排列方式");
        for (int i = 0; i < 8; i++) {
            for (int j = 0; j < 8; j++) {
                System.out.print(map[i][j] + " ");
            }
            System.out.println();
        }
        count++;
    }

    /**
     * 检验方法（验证该位置是否可以放皇后）
     */
    public static boolean check(int row, int col) {
        //上面(行减小  列不变)
        for (int i = row - 1; i >= 0; i--) {
            if (map[i][col] == 1) {
                return false;
            }
        }

        //左斜上 （行减小  列减小）
        for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {

            if (map[i][j] == 1) {
                return false;
            }

        }
        //右斜上 （行减小  列增加）
        for (int i = row - 1, j = col + 1; i >= 0 && j < 8; i--, j++) {

            if (map[i][j] == 1) {
                return false;
            }

        }
        return true;
    }

    /**
     * 八皇后算法
     */
    public static void play(int row) {

        //遍历当前行的所有单元格
        for (int i = 0; i < 8; i++) {
            //判断本格是否可以放皇后
            if (check(row, i)) {
                map[row][i] = 1;
                //判断是否为最后一行
                if (row == 7) {
                    show();
                } else {
                    //接着走下一行
                    play(row + 1);
                }

                //取消当前落子  清空棋盘
                map[row][i] = 0;
            }
        }
    }

    public static void main(String[] args) {
        play(0);
    }
}

四、总结

对于递归思想可以有如下总结：

采用递归编程最好持有“井底之蛙”的思想；
递归的特点在于：它一次只打算解决一点点的问题。

对于递归实现可以关注两点：

递归的出口条件；
归纳法中得到的规律。

我的微信公众号：架构真经（id：gentoo666），分享Java干货，高并发编程，热门技术教程，微服务及分布式技术，架构设计，区块链技术，人工智能，大数据，Java面试题，以及前沿热门资讯等。每日更新哦！

参考资料：

1、 https://blog.csdn.net/qq_41359051/article/details/85276387；
2、 https://blog.csdn.net/qq_35256722/article/details/52728739；
3、 https://blog.csdn.net/u010183728/article/details/81238401；
4、 https://blog.csdn.net/xb2355404/article/details/79144451；
5、 https://blog.csdn.net/m0_37618340/article/details/82635031；