1、哈希函数的构造方法
>数字分析法
假设关键字 Key 为 8 位十进制整数:
①确定哈希表的长度,示例:100,即地址空间为 0 ~ 99
②确定 “取值比较均匀分布” 的位置,示例:第四位和第七位
③则哈希函数为 H(Key) = H(ABCDEFGH) = DG
④示例: H(81301367) = 06、 H(81346532) = 43
>平方取中法
假设关键字 Key 为大写英文字符串:
①确定哈希表的长度,示例:1000,即地址空间为 0 ~ 999
②指定内部编码,示例: A-01, B-02, C-03 。。。 Z-20
③计算内部编码平方,取中间三位作为哈希值
| 关键字 | 内部编码 | 内部编码的平方 | H(Key)关键字的哈希地址 |
|---|---|---|---|
| KEKA | 11052501 | 122157 778 355001 | 778 |
| KYAB | 11250102 | 126564 795 010404 | 795 |
| AKEY | 01110525 | 001233 265 775625 | 315 |
>分段叠加法
假设关键字 Key 为超长的整数,示例 12360324711202065 :
①确定哈希表的长度,示例:1000,即地址空间为 0 ~ 999
②从左到右,分割成 N 个三位数,右侧不足三位的舍弃,示例:123 603 247 112 020
③将N 个三位数相加,结果超过三位数的左侧舍弃,示例:
H(Key) = H(12360324711202065) = 123 + 603 + 247 +112 + 020 = 1105 % 1000 = 105
>除留余数法
假设哈希表长 m, p 为小于等于 m 的最大素数,哈希函数为:
H(Key) = k % p
示例:key 为 80, 表长 13,最大素数 13,H(Key) = H(80) = 80 % 13 = 5
>伪随机数法
采用一个伪随机函数作为哈希函数, 即 H(key) = random(key)
2、处理冲突的方法
>开放定址法(再散列法)
关键字key 的初始哈希地址 h0 = H(key) 产生冲突时,以 h0 为基础,产生另一个地址 h1,若 h1 仍然冲突,再以 h0 为基础,产生哈希地址 h2,直到不冲突为止!
初始哈希地址:H0 = H(key)
冲突哈希地址:Hi = (H0 + Di) % m i = 1,2,...,n
①线性探测再散列
Di= 1,2,3,...,m-1
②二次探测再散列
Di= 1^2, -1^2, 2^2, -2^2,.... k^2, -k^2 (k <= m/2)
③伪随机探测再散列
Di= 伪随机数序列
查找结束条件:直到找到一个空单元或者查遍全表
>再哈希法
同时构造多个不同的哈希函数,当哈希发生冲突时,使用下一个哈希函数,直到不再产生冲突。
这种方法不易产生聚焦,但增加了计算时间!
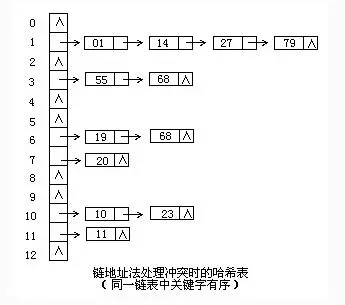
>链地址法
产生的哈希冲突加入链表
3、Java 中哈希值的计算规则
①创建 int result,赋值非0
②对于在 equals() 方法中测试的每个字段 f,通过以下方式计算哈希值 c:
- boolean: (f ? 0 : 1)
- byte, char, short 或 int: (int)f
- long: (int)(f ^ (f >>
>32)) - float: Float.floatToIntBits(f)
- double: Double.doubleToLongBits(f) 并像 long 型一样处理返回结果
- object: 使用 hashCode() 方法,若为 null 返回 0
- array: 将每个字段视为单独的元素并以递归方式计算哈希值,并按照下面所述方式组合最终结果
③组合哈希值 c 和 result
result = 37 * result + c
④返回 result
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: