程序员的算法课（10）-字符串排序算法实例（纯代码）

一、低位优先（Least-Signifcant-Digit First，LSD）

字符串的低位优先排序算法目的就是将一组字符串按照从右到左的顺序依次比较指定索引位置的字符大小并排序。根据上述字符串的分组算法的逻辑，很容易使用下面的代码实现：下面的代码实质上就是将一组字符串按照倒数第一个字符分组（最后一个字符相同的，分组前后相对顺序不变），接着再按照倒数第二个字符分组（倒数第二个字符相同的，分组前后相对顺序不变），直到最终按照倒数第n个字符分组完毕。

    public static void sortByLSD(String[] a, int W) {
        int N = a.length;
        int R = 256;   // 假设字符串中的字符都来自于ASCII字母表
        String[] temp = new String[N];

        for (int d = W-1; d >= 0; d--) {
            // 对于第d个字符，按照该字符代表的数字大小对字符数组进行排序
            // 统计出现频率
            int[] count = new int[R+1];
            for (int i = 0; i < N; i++)
                count[a[i].charAt(d) + 1]++;

            // 计算放入临时数组的起始索引
            for (int r = 0; r < R; r++)
                count[r+1] += count[r];

            // 对字符串元素进行分类
            for (int i = 0; i < N; i++)
                temp[count[a[i].charAt(d)]++] = a[i];

            // 回写
            for (int i = 0; i < N; i++)
                a[i] = temp[i];
        }
    }

二、高位优先（MSD）的字符串排序

它不要求被排序的字符串等长，而且不一定需要检查所有的输入就能完成排序。该算法将从左开始向右检查字符（就像通常我们比较字符串那样），使用和快速排序类似的方法将字符串排序。
它是从左向右检查每个字符，统计字符串首字母的频率，并按其来进行归类、排序，然后对归类后的字符串：将所有首字母相同的归为一个子数组，递归地分别对这些子数组排序。精炼点说就是：

• 以首字母来排序，将数组切分成首字母相同的子数组
• 忽略都相同的首字母，递归地排序子数组

    // 返回字符串制定索引位置的字符，如果索引位置值等于字符串长度值，则返回-1
    private static int charAt(String s, int d) {
        assert d >= 0 && d <= s.length();
        if (d == s.length())
            return -1;
        return s.charAt(d);
    }

    private static void sort(String[] a, int lo, int hi, int d, String[] temp) {
        if (hi <= lo) {
            return;
        }
        int R = 256;

        // 计算出现频率
        int[] count = new int[R + 2];// 加2是因为把超出字符串索引找不到的字符也当做一个字符，注意低位优先算法是+1
        for (int i = lo; i <= hi; i++) {
            int c = charAt(a[i], d);
            count[c + 2]++;
        }

        // 计算迁移到临时数组的起始索引
        for (int r = 0; r < R + 1; r++)
            count[r + 1] += count[r];

        // 对字符串进行分类
        for (int i = lo; i <= hi; i++) {
            int c = charAt(a[i], d);
            temp[count[c + 1]++] = a[i];
        }

        // 回写
        for (int i = lo; i <= hi; i++)
            a[i] = temp[i - lo];

        // 递归的以各个字符进行分类
        for (int r = 0; r < R; r++)
            sort(a, lo + count[r], lo + count[r + 1] - 1, d + 1, temp);
    }

    // 交换a[i] 与 a[j] 两个字符串
    private static void exch(String[] a, int i, int j) {
        String temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

    public static void sortByMSD(String[] a) {
        int N = a.length;
        String[] temp = new String[N];
        sort(a, 0, N - 1, 0, temp);
    }

    public static void main(String... args) {
        String[] a = new String[] { "aaaabbbb", "bbbbbbbb", "ccccdddd", "ccccaaaa" };
        sortByMSD(a);
        System.out.println(Arrays.toString(a));

    }

三、三向快速的字符串排序 （扩展）

快速排序在实际应用中会面对大量具有重复元素的数组，因此我们可以改进排序算法，我们对键的首字母进行三向切分，然后递归地将三个子数组进行排序。三向字符串快速排序是一个字符串排序的通用算法，最多的情况适用于含有公共前缀的字符串。

三向切分是个啥：将数组分为三部分：小于当前切分元素的部分，等于当前切分元素的部分，大于当前切分元素的部分。

E.W.Dijlstra（对，就是Dijkstra最短路径算法的发明者）曾经提出一个与之相关的荷兰国旗问题（一个数组中有分别代表红白蓝三个颜色的三个主键值，将三个主键值排序，就得到了荷兰国旗的颜色排列）。

他提出的算法是： 对于每次切分：从数组的左边到右边遍历一次，维护三个指针lt,gthe i，其中

• lt指针使得元素（arr[0]-arr[lt-1]）的值均小于切分元素；
• gt指针使得元素（arr[gt+1]-arr[N-1]）的值均大于切分元素；
• i指针使得元素（arr[lt]-arr[i-1]）的值均等于切分元素，（arr[i]-arr[gt]）的元素还没被扫描，切分算法执行到i>gt为止。

每次切分之后，位于gt指针和lt指针之间的元素的位置都已经被排定，不需要再去移动了。之后将（lo,lt-1）,（gt+1,hi）分别作为处理左子数组和右子数组的递归函数的参数传入，递归结束，整个算法也就结束。
三向切分的示意图：

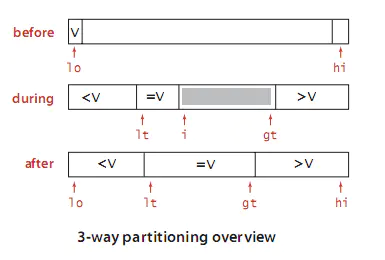
代码如下：

    public static void sort(String[] a) {
        sort(a, 0, a.length-1, 0);
    }

    private static int charAt(String s, int d) { 
        assert d >= 0 && d <= s.length();
        if (d == s.length()) return -1;
        return s.charAt(d);
    }

    //对a[lo..hi]范围的字符按照第d个字符排序或分类
    private static void sort(String[] a, int lo, int hi, int d) { 

        if (hi <= lo) {
            return;
        }

        int lt = lo, gt = hi;
        int v = charAt(a[lo], d);
        int i = lo + 1;
        while (i <= gt) {
            int t = charAt(a[i], d);
            if      (t < v) exch(a, lt++, i++);
            else if (t > v) exch(a, i, gt--);
            else              i++;
        }

        /*
         *看下面的代码，知道为什么称为三向排序了吧？ 
         */
        sort(a, lo, lt-1, d);  //排序a[lo..lt-1]返回的字符串
        if (v >= 0) sort(a, lt, gt, d+1); //排序a[lt..gt]范围的字符串
        sort(a, gt+1, hi, d); //排序a[gt+1..hi]范围的字符串
    }

    private static void exch(String[] a, int i, int j) {
        String temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

    public static void main(String[] args) {
        String[] a = new String[] { "aaaabbbb", "bbbbbbbb", "ccccdddd", "ccccaaaa" };
        sort(a);
        System.out.println(Arrays.toString(a));
    }

相对于高位优先字符串算法的优点：

1、 高位优先字符串算法可能会创建许多的空数组（前缀相同的情况下），但本算法总是只有三个；
2、 本算法不需要额外的空间；
3、 要将含有N个字符串的数组排序，三向字符串快速排序需要比较字符~NlnN次；
4、 对于包含大量重复元素的数组，这个算法将排序时间从线性对数级降到了线性级别；

我的微信公众号：架构真经（id：gentoo666），分享Java干货，高并发编程，热门技术教程，微服务及分布式技术，架构设计，区块链技术，人工智能，大数据，Java面试题，以及前沿热门资讯等。每日更新哦！

参考资料：

1、 https://blog.csdn.net/nmgrd/article/details/52014235；
2、 https://www.cnblogs.com/xiaofeixiang/p/4857404.html；
3、 https://cloud.tencent.com/developer/article/1139660；
4、 https://www.jianshu.com/p/d70aeccaee19；

版权声明：本文不是「本站」原创文章，版权归原作者所有 | 原文地址: