文章目录
- 前言
- 一、常用查找算法
- 二、顺序(线性)查找算法
-
- 2.1 问题描述
- 2.2 代码实现
- 2.3 测试结果
- 三、二分查找(折半查找)算法
-
- 3.1 问题描述
- 3.2 查找思路
- 3.3 二分查找代码实现
- 3.4 测试结果
- 3.5 课后完善
-
- 3.5.1 问题描述
- 3.5.2 代码实现
- 四、差值查找算法
-
- 4.1 原理介绍
- 4.2 问题描述
- 4.3 代码实现
- 4.4 测试结果
- 4.5 插值查找注意事项
- 五、斐波那契算法【有点难】
-
- 5.1 斐波那契(黄金分割法)
- 5.2 斐波那契(黄金分割法)原理
- 5.3 应用实例
- 5.4 代码实现
- 5.5 结果测试
前言
一、常用查找算法
在java中,我们常用的查找有四种:
1、 顺序(线性)查找;
2、 二分查找/折半查找;
3、 插值查找;
4、 斐波那契查找【比较难】;
二、顺序(线性)查找算法
2.1 问题描述
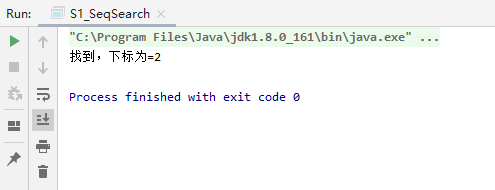
有一个数列: {1,8, 10, 89, 1000, 1234} ,判断数列中是否包含此名称【顺序查找】 要求: 如果找到了,就提示找到,并给出下标值。
2.2 代码实现
package com.feng.ch10_search;
/*
* 线性查找
* 1、没有顺序的数组
* 2、 直接循环遍历、比较
* */
public class S1_SeqSearch {
public static void main(String[] args) {
int array[] = {
1, 9, 11, -1, 34, 89}; // 没有顺序的数组
int i = seqSearch(array, 11);
if (-1 == i) {
System.out.println("没有找到");
} else {
System.out.println("找到,下标为=" + i);
}
}
/*
* 这里我们实现的线性查找是找到一个满足条件的值,就返回
* @param array
* @param num
* @return
* */
public static int seqSearch(int[] array, int num) {
for (int i = 0; i < array.length; i++) {
if (num == array[i]) {
return i;
}
}
return -1;
}
}
2.3 测试结果
三、二分查找(折半查找)算法
3.1 问题描述
请对一个有序数组进行二分查找 {1,8, 10, 89, 1000, 1234} ,输入一个数看看该数组是否存在此数,并且求出下标,如果没有就提示"没有这个数"。
3.2 查找思路
1、 首先确定该数组的中间的下标;
mid = (left + right) / 2
2、 然后让需要查找的数findVal和arr[mid]比较;
3、 1findVal>arr[mid],说明你要查找的数在mid的右边,因此需要递归的向右查找;
3、 2findVal<arr[mid],说明你要查找的数在mid的左边,因此需要递归的向左查找;
3、 3findVal==arr[mid]说明找到,就返回;
什么时候我们需要结束递归.
1、 找到就结束递归;
2、 递归完整个数组,仍然没有找到findVal,也需要结束递归当left>right就需要退出;

3.3 二分查找代码实现
package com.feng.ch10_search;
import java.util.ArrayList;
import java.util.Arrays;
/*
* 二分查找:
* 注意:使用二分查找的前提是 该数组是有序的.
* 1、递归算法方式
* java.lang.StackOverflowError : 死循环
*
* 2、非递归方式
* */
public class S2_BinarySearch {
public static void main(String[] args) {
int array[] = {
1, 8, 10, 89, 1000, 1000, 1234};
System.out.println("数组为:");
System.out.println(Arrays.toString(array));
System.out.println();
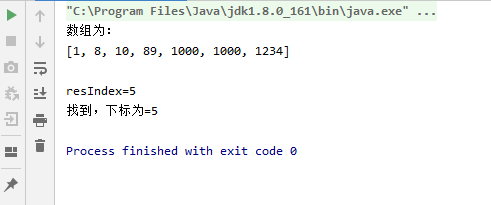
int resIndex = binarySearchOne(array, 0, array.length - 1, 1000);
// ArrayList resIndex = binarySearchAllElement(array, 0, array.length - 1, 1000);
System.out.println("resIndex=" + resIndex);
if (resIndex == -1) {
System.out.println("没有找到");
} else {
System.out.println("找到,下标为=" + resIndex);
}
}
/*
* 二分查找算法
* 注意点:
*
*
* @param array 需要查找的数组
* @param left 左边的索引
* @param right 右边的索引
* @param findVal 如果找到就返回下标,如果没有找到,就返回 -1
* */
public static int binarySearchOne(int[] array, int left, int right, int findVal) {
/*
* 当 left > left 时,说明递归整个数组,但是没有找到,
* */
if (left > right) {
return -1;
}
int mid = (left + right) / 2;
int midVal = array[mid];
if (findVal > midVal) {
// 向右递归
return binarySearchOne(array, mid + 1, right, findVal);
} else if (findVal < midVal) {
// 向左递归
return binarySearchOne(array, left, mid - 1, findVal);
} else {
return mid;
}
}
}
3.4 测试结果
3.5 课后完善
3.5.1 问题描述
课后思考题: {1,8, 10, 89, 1000, 1000,1234} 当一个有序数组中,有多个相同的数值时,如何将所有的数值都查找到,比如这里的 1000.
3.5.2 代码实现
/*
* 完成一个 课后思考题
* {1,8, 10, 89, 1000, 1000,1234} 当一个有序数组中,有多个相同的数值时,如何将所有的数值都查找到,比如这里的 1000.
*
* 思路分析
* 1、在找到 mid 值时,不要马上返回,
* 2、向 mid 索引值的左边扫描,将所有满足 1000 的元素的下标,加入到集合 ArrayList
* 3、向 mid 索引值 的右边扫描,将所有满足 1000 的元素的下标,加入到集合 ArrayList
* 4、 将 ArrayList 返回即可
* */
/*
* @param array 需要查找的数组
* @param left 左边的索引
* @param right 右边的索引
* @param findVal 如果找到就返回下标,如果没有找到,就返回 -1
* */
public static ArrayList<Integer> binarySearchAllElement(int[] array, int left, int right, int findVal) {
System.out.println("此句话每打印几次,说明调用查询方法几次");
/*
* 当 left > left 时,说明递归整个数组,但是没有找到,
* */
if (left > right) {
return new ArrayList<Integer>();
}
int mid = (left + right) / 2;
int midVal = array[mid];
if (findVal > midVal) {
// 向右递归
return binarySearchAllElement(array, mid + 1, right, findVal);
} else if (findVal < midVal) {
// 向左递归
return binarySearchAllElement(array, left, mid - 1, findVal);
} else {
/*
* 代码走到这里时,为 findVal == midVal , 原来是 直接返回 下标 mid 即可。现在是有可能是重复了几个值,
* 所以这里要对这个 mid下标 的左右两边进行遍历,比较
*
* 思路分析
* 1、在找到 mid 值时,不要马上返回,
* 2、向 mid 索引值的左边扫描,将所有满足 1000 的元素的下标,加入到集合 ArrayList
* 3、向 mid 索引值 的右边扫描,将所有满足 1000 的元素的下标,加入到集合 ArrayList
* 4、 将 ArrayList 返回即可
* */
ArrayList<Integer> resIndexList = new ArrayList<>();
// 2、向 mid 索引值的左边扫描,将所有满足 1000 的元素的下标,加入到集合 ArrayList
int temp = mid - 1;
while (true) {
if (temp < 0 || array[temp] != findVal) {
// 退出
break;
}
// 否则 ,就把 temp 放入到 resIndexList 集合中
resIndexList.add(temp);
temp -= 1; // temp 左移
}
// 别忘了 把 mid 这个下标添加到 集合 中
resIndexList.add(mid);
//3、向 mid 索引值 的右边扫描,将所有满足 1000 的元素的下标,加入到集合 ArrayList
temp = mid + 1;
while (true) {
if (temp > array.length - 1 || array[temp] != findVal) {
// 退出
break;
}
// 否则 ,就把 temp 放入到 resIndexList 集合中
resIndexList.add(temp);
temp += 1; // temp 右移
}
return resIndexList;
}
}
四、差值查找算法
4.1 原理介绍
1、 插值查找算法类似于二分查找,不同的是插值查找每次从自适应mid处开始查找;
2、 将折半查找中的求mid索引的公式,low表示左边索引left,high表示右边索引right.key就是前面我们讲的findVal;

3、 intmid=low+(high-low)*(key-arr[low])/(arr[high]-arr[low]);插值索引对应前面的代码公式:;
int mid = left + (right – left) * (findVal – arr[left]) / (arr[right] – arr[left])
4、 举例说明插值查找算法1-100的数组;

4.2 问题描述
请对一个有序数组进行插值查找 {1,8, 10, 89, 1000, 1234} ,输入一个数看看该数组是否存在此数,并且求出下标,如果没有就提示"没有这个数"。
4.3 代码实现
package com.feng.ch10_search;
import java.util.Arrays;
/*
* 差值查找算法
*
* */
public class S3_InsertValueSearch {
public static void main(String[] args) {
int[] array = new int[100];
for (int i = 0; i < 100; i++) {
array[i] = i + 1;
}
System.out.println("数组为:");
System.out.println(Arrays.toString(array));
System.out.println();
int i = insertValueSearch(array, 0, array.length - 1, 66);
if (-1 == i) {
System.out.println("找不到");
} else {
System.out.println("找到了,下标为:" + i);
}
}
public static int insertValueSearch(int[] array, int left, int right, int findVal) {
System.out.println("此句话每打印几次,说明调用查询方法几次");
/*
* 注意: left > right 和 findVal < array[0] 和 findVal > array[array.length-1] 必须需要
* 否则我们得到的 mid 可能 越界
* */
if (left > right || findVal < array[0] || findVal > array[array.length - 1]) {
return -1;
}
// 求出 mid
int mid = left + (right - left) * (findVal - array[left]) / (array[right] - array[left]);
int midVal = array[mid];
if (findVal > midVal) {
// 向右递归
return insertValueSearch(array, mid + 1, right, findVal);
} else if (findVal < midVal) {
// 向左递归
return insertValueSearch(array, left, mid - 1, findVal);
} else {
return mid;
}
}
}
4.4 测试结果

4.5 插值查找注意事项
1、 对于数据量较大,关键字分布比较均匀的查找表来说,采用插值查找,速度较快.;
2、 关键字分布不均匀的情况下,该方法不一定比折半查找要好;
五、斐波那契算法【有点难】
5.1 斐波那契(黄金分割法)
1、 黄金分割点是指把一条**线段**分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比取其前三位数字的近似值是0.618由于按此比例设计的造型十分美丽,因此称为黄金分割,也称为中外比这是一个神奇的数字,会带来意向不大的效果;
2、 斐波那契数列{1,1,2,3,5,8,13,21,34,55}发现斐波那契数列的两个相邻数的比例,无限接近黄金分割值0.618;
5.2 斐波那契(黄金分割法)原理
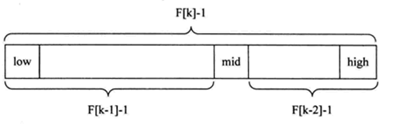
- 斐波那契查找原理与前两种相似,仅仅改变了中间结点(mid)的位置,mid不再是中间或插值得到,而是位于黄金分割点附近,即mid=low+F(k-1)-1(F代表斐波那契数列),如下图所示
- 对F(k-1)-1的理解:
1、 由斐波那契数列F[k]=F[k-1]+F[k-2]的性质,可以得到(F[k]-1)=(F[k-1]-1)+(F[k-2]-1)+1该式说明:只要顺序表的长度为F[k]-1,则可以将该表分成长度为F[k-1]-1和F[k-2]-1的两段,即如上图所示从而中间位置为mid=low+F(k-1)-1;
2、 类似的,每一子段也可以用相同的方式分割;
3、 但顺序表长度n不一定刚好等于F[k]-1,所以需要将原来的顺序表长度n增加至F[k]-1这里的k值只要能使得F[k]-1恰好大于或等于n即可,由以下代码得到,顺序表长度增加后,新增的位置(从n+1到F[k]-1位置),都赋为n位置的值即可;

5.3 应用实例
请对一个有序数组进行斐波那契查找 {1,8, 10, 89, 1000, 1234} ,输入一个数看看该数组是否存在此数,并且求出下标,如果没有就提示"没有这个数"。
5.4 代码实现
package com.feng.ch10_search;
import java.util.Arrays;
/*
* 斐波那契(黄金分割法)查找算法
* */
public class S4_FibonacciSearch {
public static int maxSize = 20;
public static void main(String[] args) {
int[] array = {
1, 8, 10, 89, 1000, 1234};
System.out.println("数组为:");
System.out.println(Arrays.toString(array));
System.out.println();
System.out.println("斐波那契数列:");
System.out.println(Arrays.toString(fib()));
System.out.println();
System.out.println("开始查找数据");
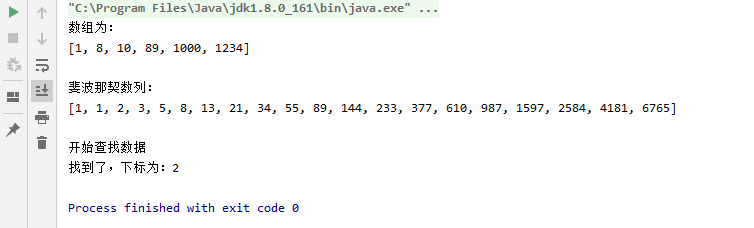
int i = fibSearch(array, 10);
if (-1 == i) {
System.out.println("没有找到");
} else {
System.out.println("找到了,下标为:" + i);
}
}
/*
* 因为后面我们 mid = low + F(k-1)-1, 需要使用到斐波那契数列,因此我们需要先获取一个斐波那契数列
* 非递归方法得到一个斐波那契数列
* */
public static int[] fib() {
int[] f = new int[maxSize];
f[0] = 1;
f[1] = 1;
for (int i = 2; i < maxSize; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
/*
* 编写斐波那契查找算法
* 使用非递归的方式编写算法
*
* @param array 数组
* @param key 我们需要查找的关键码(值)
* @return 返回对应的下标,如果没有返回 -1
* */
public static int fibSearch(int[] array, int key) {
int low = 0; // 数组 最左侧下标
int high = array.length - 1; // 数组最右侧下标 5
int k = 0; //表示斐波那契 分割数值 的下标 // mid = low + F(k-1)-1 中的 k
int mid = 0; // 存放 mid 值
int fib[] = fib(); // 获取斐波那契数列 1 1 2 3 5 8 13 21
// 获取到 斐波那契分割数值的下标
while (high > fib[k] - 1) {
// 只要条件 成立,就说明没有找到, 继续K++, 只要条件不成立,说明找到了 下标 K , 当 k = 5 时,fib[k] - 1= 8,
k++;
}
// 因为 f[k] 值,可能大于 array 的长度,因此我们需要使用 Arrays 类,构造一个新的数组,并指向 temp[]
// 不足的部分会使用 0 填充
int[] temp = Arrays.copyOf(array, fib[k]); // fib[k] 为长度
/*
* 实际上需求使用 array 数组最后的数填充 temp
* 举例:
* temp = {1,8, 10, 89, 1000, 1234, 0, 0} => {1,8, 10, 89, 1000, 1234, 1234, 1234,}
* */
for (int i = high + 1; i < temp.length; i++) {
temp[i] = array[high];
}
/*
* 使用while来循环处理,找到我们的数 key
* 叙述一下 初始值:
* low = 0, high = 5, k = 5
* */
while (low <= high) {
// 只要这个条件满足,就可以找 初始化为 0<5
mid = low + fib[k - 1] - 1; // 4,2 // 这里也是对应二分查找、插值查找算法的 mid 计算方法
if (key < temp[mid]) {
//我们应该继续向数组的前面查找(左边)
high = mid - 1;
//为甚是 k--
//说明
//1. 全部元素 = 前面的元素 + 后边元素
//2. f[k] = f[k-1] + f[k-2]
//因为 前面有 f[k-1]个元素,所以可以继续拆分 f[k-1] = f[k-2] + f[k-3]
//即 在 f[k-1] 的前面继续查找 k--
//即下次循环 mid = f[k-1-1]-1
k--;
} else if (key > temp[mid]) {
// 我们应该继续向数组的后面查找(右边)
low = mid + 1;
//为什么是k -=2
//说明
//1. 全部元素 = 前面的元素 + 后边元素
//2. f[k] = f[k-1] + f[k-2]
//3. 因为后面我们有f[k-2] 所以可以继续拆分 f[k-1] = f[k-3] + f[k-4]
//4. 即在f[k-2] 的前面进行查找 k -=2
//5. 即下次循环 mid = f[k - 1 - 2] - 1
k -= 2;
} else {
//找到
//需要确定,返回的是哪个下标
if (mid <= high) {
return mid;
} else {
return high;
}
}
}
return -1;
}
}
5.5 结果测试
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: