数据结构与算法细节篇之最短路径问题：Dijkstra和Floyd算法详细描述，java语言实现。-程序员秋天

文章目录

前言
一、单源最短路径
- 1、单源最短路径问题
2、Dijkstra 初始化
- a、参数
  - b、初始化参数
  - c、算法步骤
3、Dijkstra 算法详细步骤
- a、第一轮算法执行
  - b、第二轮算法执行
  - c、第三轮算法执行
  - d、第四轮算法执行
  - e、第五轮算法执行
  - f、第六轮算法执行
4、java算法实现
二、多源最短路径
- 1、多源最短路径问题
2、Floyd初始化
- a、参数
  - b、参数初始化
  - c、算法步骤
3、Floyd算法详细步骤
4、java 算法实现

前言

最短路径的算法有两个，Dijkstra算法和 Floyd算法。
Dijkstra算法解决的是 单源最短路径问题。
Floyd算法解决的是 多源最短路径问题，并且可以处理负权图。
今天要讲的就是Dijkstra算法。
加：feng--Insist(大写的i)，进java交流群讨论互联网+技术。可索要PPT等资料。
其他资料，建议先看本篇博客。：Dijkstra算法和Floyd算法：https://blog.csdn.net/weixin_43872728/article/details/100662957
代码位置：https://github.com/fengfanli/dataStructuresAndAlgorithm/tree/master/src/com/feng/algorithm/self_learn

一、单源最短路径

1、单源最短路径问题

解决的问题: 求解单源最短路径,即各个节点到达源点的最短路径或权值。如下图中

考察其他所有节点到源点的最短路径和长度
局限性: 无法解决权值为负数的情况
资料
可先看匹配视频：https://www.bilibili.com/video/BV1o44y1B7NM/
代码：待上传。

2、Dijkstra 初始化

首先已知的是：
给定 邻接矩阵表示的图Graph、源点S、终点T。

a、参数

参数:

参数名	解释
S	记录当前已经处理过的源点到最短节点
U	记录还未处理的节点
dist[]	记录各个节点到起始节点的最短权值
path[]	记录各个节点的上一级节点(用来联系该节点到起始节点的路径)

b、初始化参数

顶点集S: 节点A到自已的最短路径长度为0。只包含源点，即S={A}，代码中没有这个，这里是为了步骤清晰而设置的。
顶点集U: 包含除A外的其他顶点. 即U={B,C,D,E,F,G}
dist[]: 源点还不能到达的节点,其权值为∞

名	A	B	C	D	E	F	G
dist[]:	0	1	2	3	4	5	6
初始化值:	0	4	6	6	∞	∞	∞

path[]: 记录当前节点的前驱节点下标(源点还不能到达的节点为-1)

名	A	B	C	D	E	F	G
path[]:	0	1	2	3	4	5	6
初始化值:	0	0	0	0	-1	-1	-1

c、算法步骤

1、初始化：设定除源节点以外的其它所有节点到源节点的距离为INFINITE(一个很大的数)，且这些节点都没被处理过如上图所示；
2、从源节点出发，更新相邻节点(图中为B、C、D)到源节点的距离然后在所有节点中选择一个最段距离的点作为当前节点；
3、标记当前节点为done(表示已经被处理过)，与步骤2类似，更新其相邻节点的距离(这些相邻节点的距离更新也叫松弛，目的是让它们与源节点的距离最小因为你是在当前最小距离的基础上进行更新的，由于当前节点到源节点的距离已经是最小的了，那么如果这些节点之前得到的距离比这个距离大的话，我们就更新它)；
4、步骤3做完以后，设置这个当前节点已被done，然后寻找下一个具有最小代价(cost)的点，作为新的当前节点，重复步骤3.；
5、如果最后检测到目标节点时，其周围所有的节点都已被处理，那么目标节点与源节点的距离就是最小距离了如果想看这个最小距离所经过的路径，可以回溯，前提是你在步骤3里面加入了当前节点的最优路径前驱节点信息；

我总结了下可用如下几句话代替：
两步走

1、从dist[]中在集合U中的选择最小距离加入到S中，作为当前节点(最小距离：就是当前节点到源点的最小距离)；
2、 遍历当前节点的邻边节点：更新dist[]和path[]；

 *  如果经过当前节点+邻边权重 < 邻边节点，则改变dist\[\]和path\[\]，否者不改变。

3、Dijkstra 算法详细步骤

a、第一轮算法执行

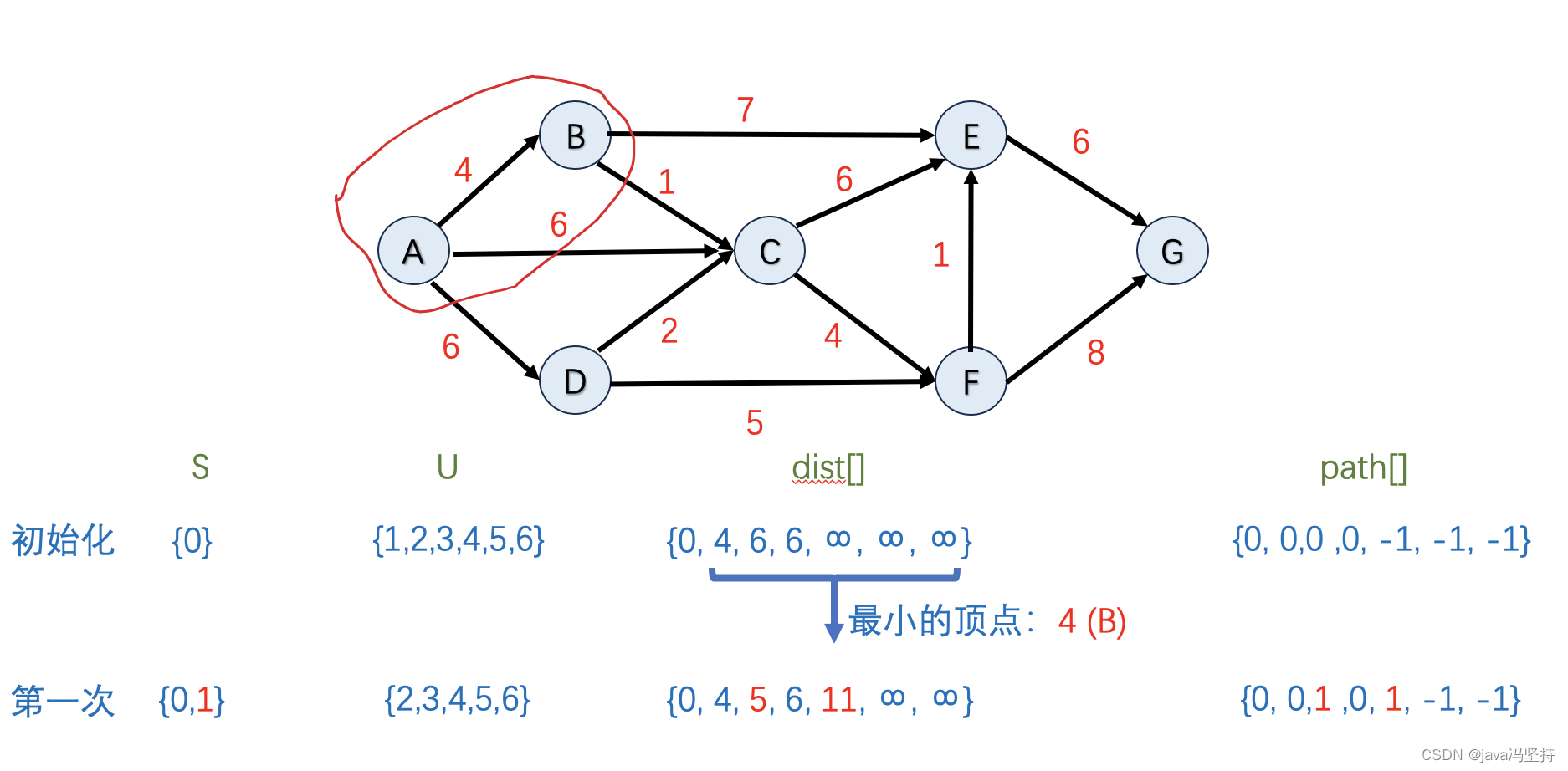
如上图，因为dist[]中排出掉集合U中节点，最小值是4，也就是节点B，所以将B纳入到集合S中（圈中）。
首先在dist[]数组中并在集合U中 最小值是节点B，既当前节点，其邻边有C和E，所以看是否要更新C和E。
节点C：因为C的最小距离dist[1](B的最小距离)4+1(B到C的距离)=5 < dist[2](C的最小距离) = 6，所以 dist[2]=5，path[2]=1
节点E：因为E的最小距离 dist[1](B的最小距离)4+7(B到E的距离)=11 < dist[4] (E的最小距离)=无穷大，所以 dist[4]=11,path[4]=1
第一轮算法两个邻边节点C、E有改变

b、第二轮算法执行

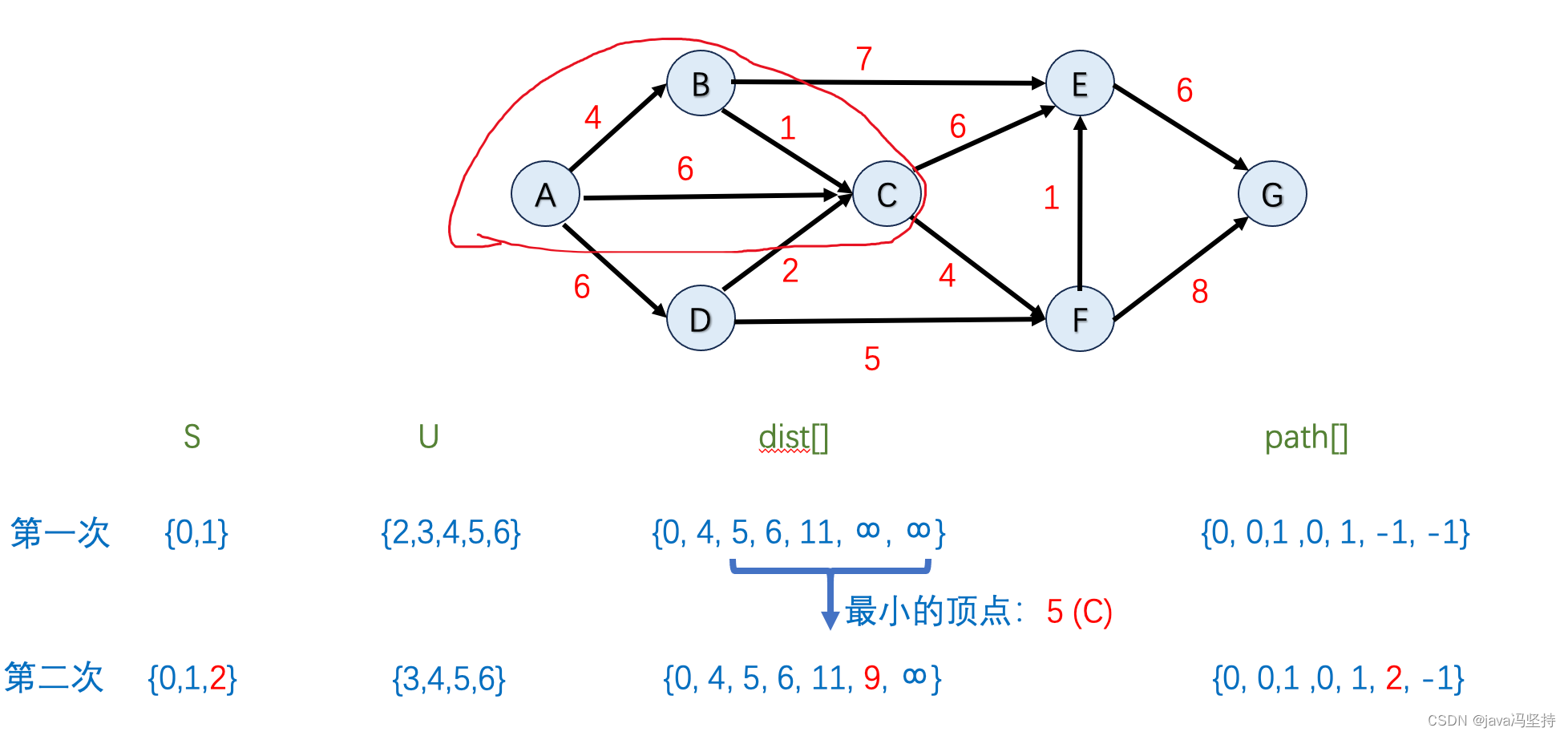
如上图，因为dist[]中排出掉集合U中节点，最小值是5，也就是节点C，所以将C纳入到集合S中（圈中）。
首先在dist[]数组中并在集合U中 最小值是节点C，既当前节点，其邻边有E和F，所以看是否要更新E和F。
节点E：因为C的最小距离 dist[2](也就是C的最小距离)5+6(C到E的距离)=11 == dist[4](E的最小距离) = 11，所以不动
节点F：因为F的最小距离 dist[2](也就是C的最小距离)5+4(C到F的距离)=9 < dist[5] (F的最小距离)=无穷大，所以 dist[5]=9,path[5]=2
第二轮算法两个邻边节点仅有 F有改变

c、第三轮算法执行

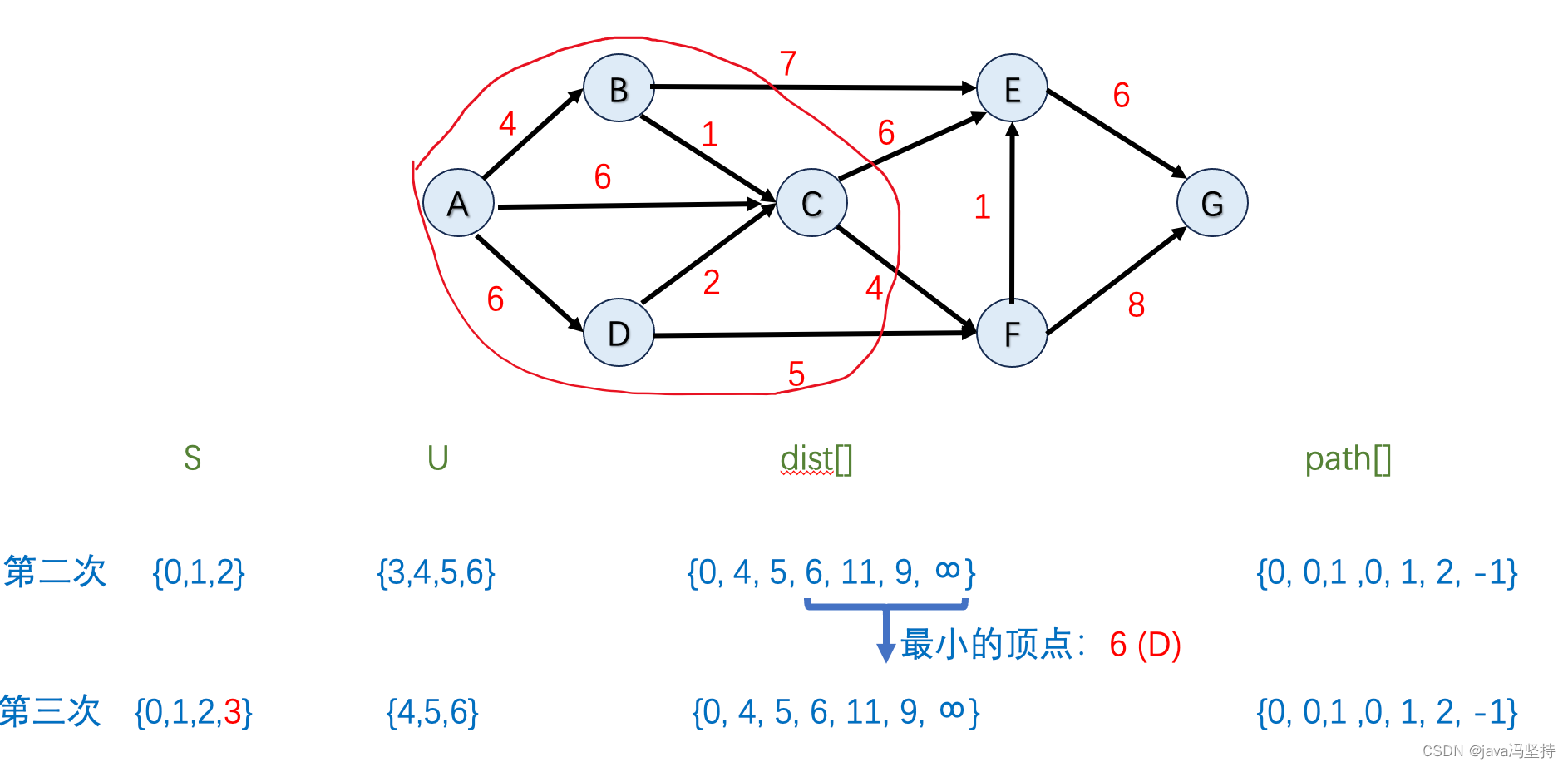
如上图，因为dist[]中排出掉集合U中节点，最小值是6，也就是节点D，所以将D纳入到集合S中（圈中）。
首先在dist[]数组中并在集合U中 最小值是节点D，既当前节点，其邻边有C和F，所以看是否要更新C和F。
节点C：因为C的最小距离 dist36+2(D到C的距离)=8 >` dist2 = 5 ，所以不动
节点F：因为F的最小距离 dist36+5(D到F的距离)=11 >` dist[5] (F的最小距离)=9，所以不动
第三轮算法两个邻边节点C、F都没有改变

d、第四轮算法执行

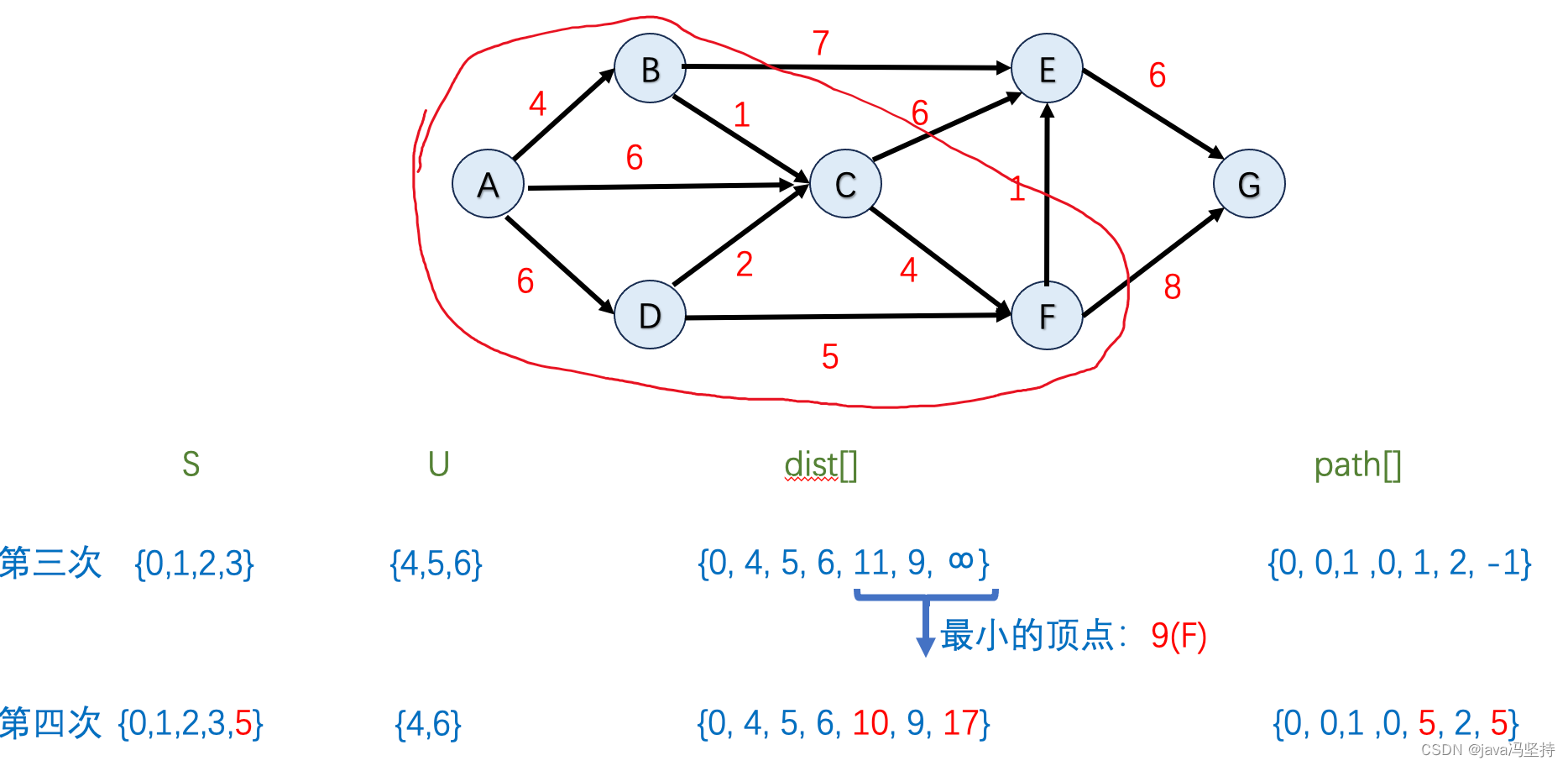
如上图，因为dist[]中排出掉集合U中节点，最小值是9，也就是节点F，所以将F纳入到集合S中（圈中）。
首先在dist[]数组中并在集合U中 最小值是节点F，既当前节点，其邻边有E和G，所以看是否要更新E和G 。
节点E：因为E的最小距离 dist5 9 +1(F到E的距离)=10 `< dist4 =11，所以 dist[4] = 10,path[4]=5
节点G：因为G的最小距离 dist5 9 +8(F到G的距离)=17 `< dist6 =无穷大，所以 dist[6]=17,path[6]=5
第四轮算法两个邻边节点E、G都有改变

e、第五轮算法执行

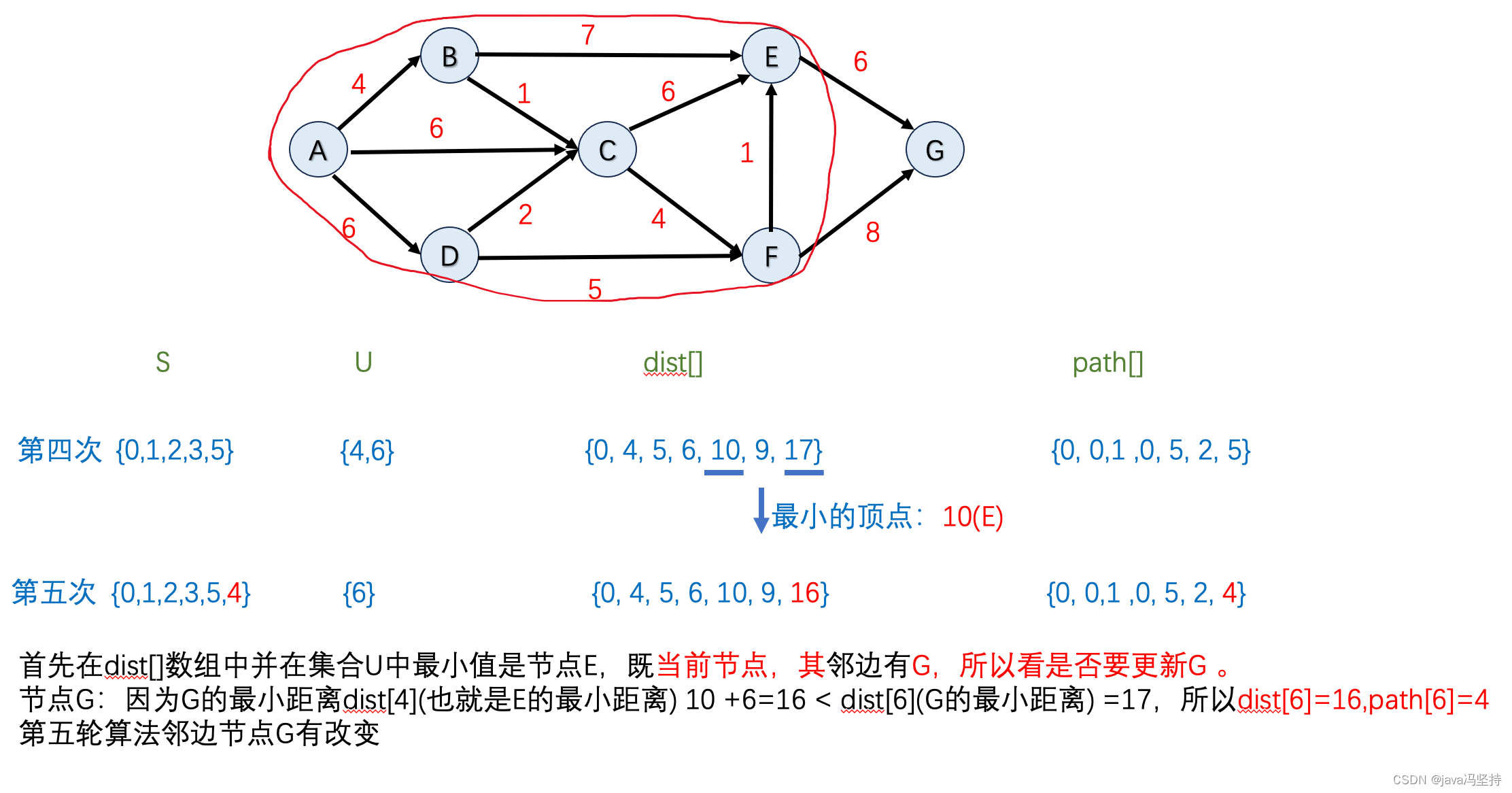
如上图，因为dist[]中排出掉集合U中节点，最小值是9，也就是节点F，所以将F纳入到集合S中（圈中）。
首先在dist[]数组中并在集合U中 最小值是节点E，既当前节点，其邻边有G，所以看是否要更新G 。
节点G：因为G的最小距离 dist4 10 +6(E到G的距离)=16 `< dist6 =17，所以 dist[6]=16,path[6]=4
第五轮算法邻边 节点G有改变

f、第六轮算法执行

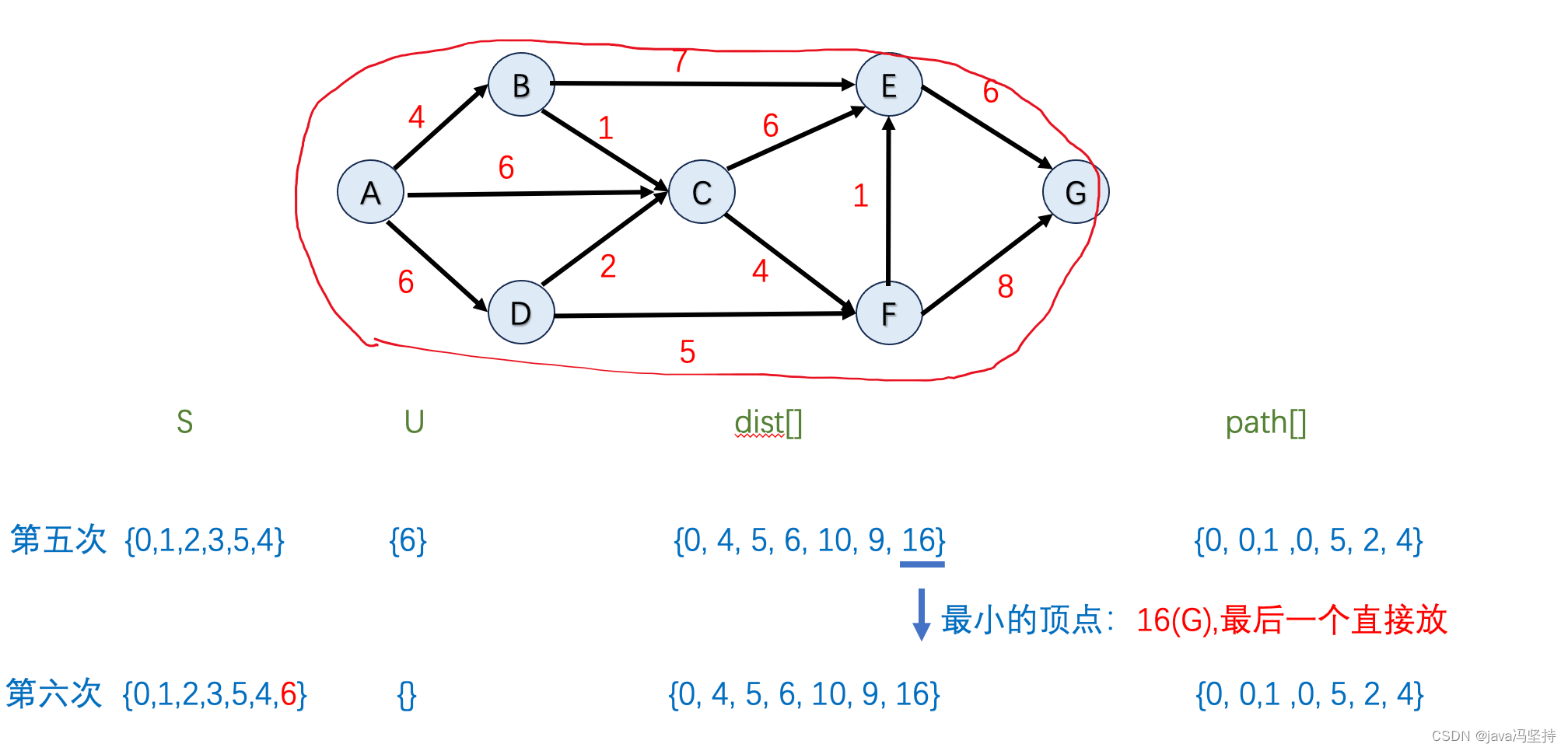
如上图，因为dist[]中排出掉集合U中节点，最小值是16，也就是节点G，所以将G纳入到集合S中（圈中）。
首先在dist[]数组中并在集合U中 最小值是节点G，既当前节点，其没有邻边。
第六轮算法邻边节点G没有改变
到此算法遍历结束

4、java算法实现

给定矩阵表示的Graph结构。输入源点v0和终点v1。

```

## 二、多源最短路径 ##

### 1、多源最短路径问题 ###

 *  上面的Dijkstra 解决的是单源最短路径的问题，首先要给定 开始节点和终止结点，如果换了开始和终止节点，那就要每次都要重新跑一次。
 *  那就引出了多源最短路径问题：就是执行一次算法，求出每两个点之间的最短距离，这就是多源最短路径算法。这个算法代码略简单一些。
 *  思想只有一个：要算两个点之间的最短距离，就看有没有第三个点使得

### 2、Floyd初始化 ###

首先已知的是：  
给定\*\*邻接矩阵表示的图Graph。

#### a、参数 ####

<table> 
<thead> 
<tr> 
<th>参数名</th> 
<th>解释</th> 
</tr> 
</thead> 
<tbody> 
<tr> 
<td>A[][]</td> 
<td>函数中的参数，需要返回，存储的是节点的前置节点。</td> 
</tr> 
<tr> 
<td>path[][]</td> 
<td>存储的是每两点之间的所需距离。</td> 
</tr> 
</tbody> 
</table>

#### b、参数初始化 ####

<table> 
<thead> 
<tr> 
<th>参数名</th> 
<th>解释</th> 
</tr> 
</thead> 
<tbody> 
<tr> 
<td>A[][]</td> 
<td>就是图的赋值，从代码中可以看出，比较简单</td> 
</tr> 
<tr> 
<td>path[][]</td> 
<td>默认都是-1.表示从A点到B点是直达的。</td> 
</tr> 
</tbody> 
</table>

#### c、算法步骤 ####

**1、** 对于每个顶点`v`（体现在代码的第一层for循环），和任意一顶点`（i,j）`(体现代码的第二、三层循环),切`i!=j、v!=i、v!=j`；  
**2、** 如果`A[i][j]>A[i][v]+A[]v[j]`，则将`A[i][j]更新为A[i][v]+A[v][j]`的值，并且将`path[i][j]改为v`；  

### 3、Floyd算法详细步骤 ###

### 4、java 算法实现 ###

```java 
package com.feng.algorithm.self_learn.floyd.floyd1;

/**
 * 学习视频：https://www.bilibili.com/video/BV1LE411R7CS
 */
public class FloydAlgorithm {

    public static void main(String[] args) {

        int[][] graph = new int[4][4];
        int N = Short.MAX_VALUE;
        graph[0] = new int[]{

     0, 5, N, 7};
        graph[1] = new int[]{

     N, 0, 4, 2};
        graph[2] = new int[]{

     3, 3, 0, 2};
        graph[3] = new int[]{

     N, N, 1, 0};

        int[][] path = new int[4][4];
        int[][] A = Floyd.floyd(graph, path);
        int u = 1;
        int v = 0;
        Floyd.printPath(u, v, path);
        System.out.println();
        System.out.println(u + "->" + v +" shortest path is :" + A[u][v]);
    }
}
class Floyd {

    /**
     * 佛洛依德算法，给定邻接矩阵表示的图，
     * path[][]:存放路径中间的节点，如果是-1就是直达
     * A[][]:存放任意两个节点之间的距离
     * 举例：从1-0，从A得出距离是6，从path得出 1-3-2-0
     * @param graph
     * @param path
     */
    static int[][] floyd(int[][] graph, int[][] path) {

        int n = graph.length;
        int v, i, j;
        int[][] A = new int[n][n];
        for (i = 0; i < n; i++) {

            for (j = 0; j < n; j++) {

                A[i][j] = graph[i][j];
                path[i][j] = -1;
            }
        }

        for (v = 0; v < n; v++) {

            for (i = 0; i < n; i++) {

                for (j = 0; j < n; j++) {

                    if (A[i][j] > A[i][v] + A[v][j]) {

                        A[i][j] = A[i][v] + A[v][j];
                        path[i][j] = v;
                    }
                }
            }
        }
        return A;
    }

    /**
     * 递归打印路径
     * @param u
     * @param v
     * @param path
     */
    static void printPath(int u, int v, int[][] path) {

        if (path[u][v] == -1) {

      // 如果等于 -1 。说明就是直达的
            System.out.printf(u + "->" + v + " ");
        } else {

            int mid = path[u][v];
            printPath(u, mid, path);
            printPath(mid, v, path);
        }
    }
}